根據CAR Theorem解決問題的重要程序步驟:(1) Criticality:探討問題的本質 (2) Abstraction:抽象化簡化問題。 (3) Restriction:將範圍縮小，首要解決的優先，次要的因子後探討。

我們利用Graph來表示物件(object)之間的關係，其中Grapg的組成需由點(Nodes)與線(Edge)來促成，利用符號表示成G=(V,E)而e={u,v}。當Graph具有方向性時{u,v} == {v,u};當Grapg不具有方向性(u,v)!=(v,u)。

生活中常見以graph來解決問題的表示方式有很多，台灣的捷運地圖就是一個很好的例子: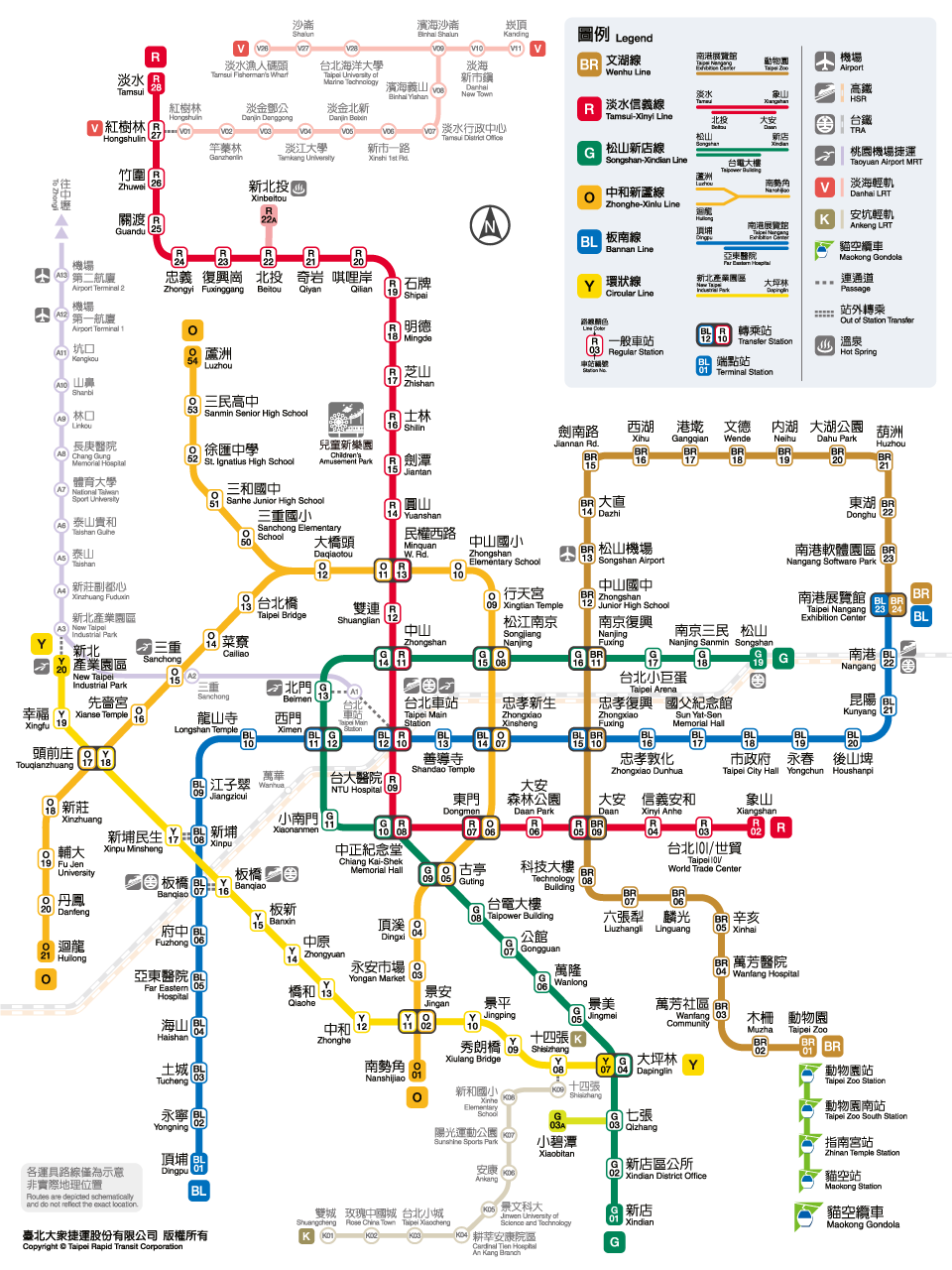

而社交網絡的表示方式，則是將原本抽象概念的思維形象化:

儘管Nodes與Edges的組成，很大的程度上解決了我們需要知道是否為neighbor的事實，卻無法藉由Edge的長度去知道交通時間，然而若是一張航海地圖，比例尺能夠有根據地調整之下，兩地之間的遠距就能夠被計算出來。

接下來我們介紹path的概念，假設P= <v1,v2,v3,v4...,vn, vn+1...>，Path上兩個連續的點之間以Edge組成，若兩個相同的起點與終點之間有無限多個走法，當我們需要找尋最小的距離(最短路徑)，則此時我們正在求最少的Edges，假使一個路徑中沒有重複相同的點，我們稱之為Simple;若兩個點有重複形成一個圓，曾稱之為Circle。

倘若我們的Grapg是一個Tree形狀，透過rooted tree可以清楚看到Nodes之間的聯繫關係，在這裡稱連結下一個點的前一個nodes為parents，也就是他們之間具有關係。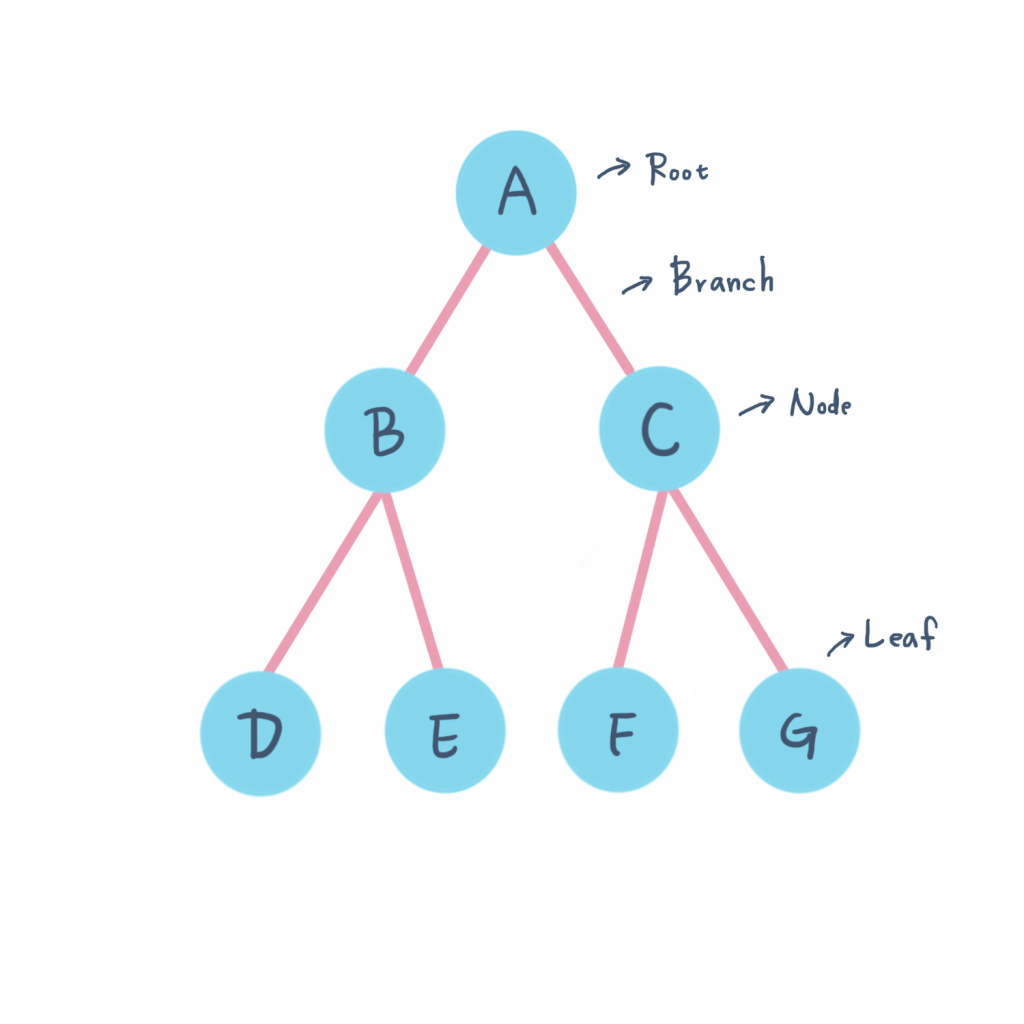

廣度優先搜尋 Breadth-First Search(BFS)
以上圖的連通元件(Connected Component)做舉例，假如我們以1為圓心漣漪式地向外擴散為搜尋的範圍，從圖示中可發現A為搜尋時間L0之內能夠抵達的範圍，B和C為L1時間內的搜尋範圍...以此類推。這些相鄰節點(adjacent nodes)只要有和圓心1有connectivity的關係，就會被BFS搜尋到，藉由此搜尋方法能夠找到從源頭至目的點的最少Edges，也就是最短路徑，值得一提的是，兩個Nodes之間的layer只差1。ex.小畫家水桶塗色

from collections import deque
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': ['E'],
    'E': ['G'],
    'F': ['G'],
    'G': []
}

def bfs_shortest_path(graph, start, goal):
    #初始化
    queue = deque([start])
    #路徑字典
    predecessor = {start: None}
    #訪問點集合
    visited = set([start])

    while queue:
        current = queue.popleft()

        # 如果找到目標節點建構路徑
        if current == goal:
            path = []
            while current is not None:
                path.append(current)
                current = predecessor[current]
            return path[::-1]  # 反转路径

        #遍佈neighbor
        for neighbor in graph[current]:
            if neighbor not in visited:
                visited.add(neighbor)
                predecessor[neighbor] = current
                queue.append(neighbor)

    return None  #如果沒有找到路徑

#使用BFS找到A到E的最短路徑
path = bfs_shortest_path(graph, 'A', 'E')
print("The shortest path from A to E is:", path)

深度優先搜尋 Depth-First Search(DFS)
從區分點(Vertex)出發，只要有路(Edges)就會往前繼續行走，以數字較小的做優先探索，若無路可進則走回去繼續進行DFS搜尋，直到無法再繼續Explore，則會Return繼續進行搜索工作，直到全部都搜索過一遍。

def dfs_path(graph, start, goal):
    #初始化
    stack = [start]
    #路徑字典
    predecessor = {start: None}
    #訪問點集合
    visited = set([start])

    while stack:
        current = stack.pop()

        #找到目標節點建構路徑
        if current == goal:
            path = []
            while current is not None:
                path.append(current)
                current = predecessor[current]
            return path[::-1]  #反轉

        #遍歷neighbor
        for neighbor in graph[current]:
            if neighbor not in visited:
                visited.add(neighbor)
                predecessor[neighbor] = current
                stack.append(neighbor)

    return None  #如果未找到路徑

#使用DFS找到A到E路徑
path = dfs_path(graph, 'A', 'E')
print("The path from A to E found by DFS is:", path)

在BFS之中的graph，為路徑的edges稱之為Tree Edge，一般來說通常為parent-child關係;反之稱為Non-Tree Edge，一般來說為uncle-nephew或是sister-brother關係。在DFS之中的graph，為路徑的edges稱之為Tree Edge，一般來說通常為parent-child關係;反之稱為Non-Tree Edge，一般來說為ancestor-descendants。下圖清楚說明BFS Tree與DFS Tree的探索路徑差異: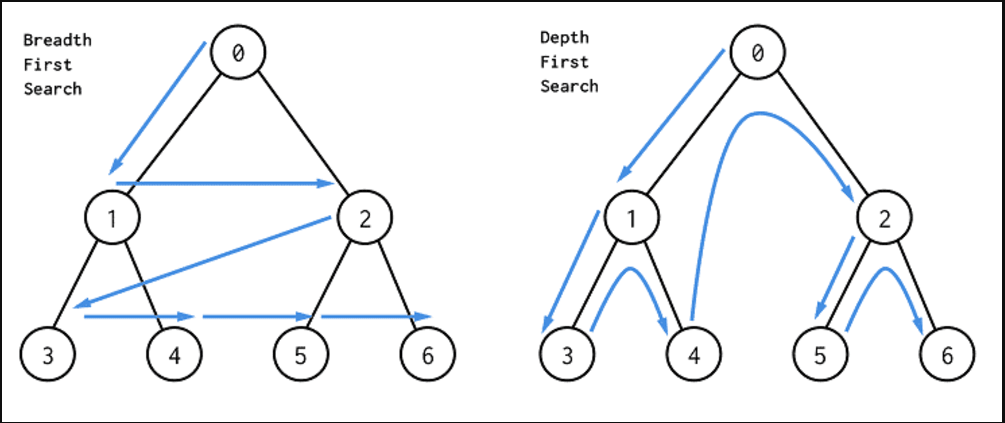

接下來我們介紹Queue&Stack來建造資料結構，之後會常常看到:
Queue
需要服從FIFO(First in,First out)規則，在Q=(a1,a2,a3...an,an+1)含有元素的情形下，我們稱a1為front，an為rear，當我們新增(push)一個資料進入會從尾巴開始，當我們刪除(pop)一個資料會從頭開始處理。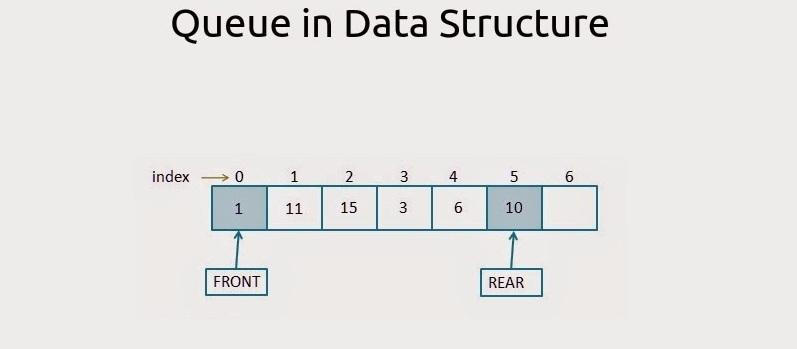

Stack
需要服從LIFO(Last in,First out)規則，最先進去的需要出去(pop)才能將新的資料push in。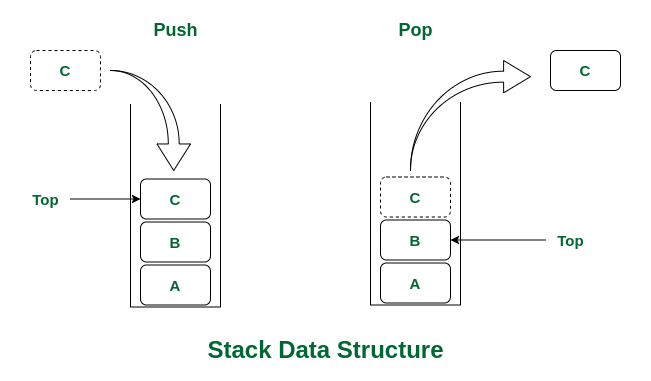

今天的文章就到這裡，下個章節會更精彩哦～